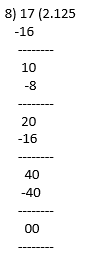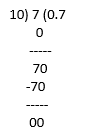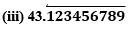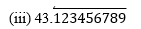Prepared By : Kalu Charan Maharana
Chapter 1
Notes
Real Numbers
Positive integers, negative integers, irrational numbers, and fractions are all examples of real numbers. In other words, we can say, any number is a real number, except complex numbers. Examples of real numbers include -1, ½, 1.75, √2, and so on.
In general,
Real numbers constitute the union of all rational and irrational numbers.Any real number can be plotted on the number line. Euclid’s Division Lemma
- Euclid’s Division Lemma states that given two integers a and b, there exists a unique pair of integers q and r such that a=b×q+r and 0≤r<b.
- This lemma is essentially equivalent to : dividend = divisor × quotient + remainder
- In other words, for a given pair of dividend and divisor, the quotient and remainder obtained are going to be unique.
Euclid’s Division Algorithm
- Euclid’s Division Algorithm is a method used to find the H.C.F of two numbers, say a and b where a> b.
- We apply Euclid’s Division Lemma to find two integers q and r such that a=b×q+r and 0≤r<b.
- If r = 0, the H.C.F is b, else, we apply Euclid’s division Lemma to b (the divisor) and r (the remainder) to get another pair of quotient and remainder.
- The above method is repeated until a remainder of zero is obtained. The divisor in that step is the H.C.F of the given set of numbers.
Prime Factorisation
- Prime Factorisation is the method of expressing a natural number as a product of prime numbers.
- Example: 36=2×2×3×3 is the prime factorisation of 36.
Fundamental Theorem of Arithmetic
- The Fundamental Theorem of Arithmetic states that the prime factorisation for a given number is unique if the arrangement of the prime factors is ignored.
- Example: 36=2×2×3×3 OR, 36=2×3×2×3
- Therefore, 36 is represented as a product of prime factors (Two 2s and two 3s) ignoring the arrangement of the factors.
Method of Finding LCM
As we know, the smallest of the common multiples of two or more numbers is called the lowest common multiple (LCM).
Example: To find the Least Common Multiple (L.C.M) of 36 and 56,
- 36=2×2×3×3
56=2×2×2×7 - The common prime factors are 2×2
- The uncommon prime factors are 3×3 for 36 and 2×7 for 56.
- LCM of 36 and 56 = 2×2×3×3×2×7 which is 504
Method of Finding HCF
We know that, the greatest number that divides each of the given numbers without leaving any remainder is the highest common factor (HCF) of two or more given numbers.
H.C.F can be found using two methods – Prime factorisation and Euclid’s division algorithm.
- Prime Factorisation:
- Given two numbers, we express both of them as products of their respective prime factors. Then, we select the prime factors that are common to both the numbers
- Example – To find the H.C.F of 20 and 24
20=2×2×5 and 24=2×2×2×3 - The factor common to 20 and 24 is 2×2, which is 4, which in turn is the H.C.F of 20 and 24.
- Euclid’s Division Algorithm:
- It is the repeated use of Euclid’s division lemma to find the H.C.F of two numbers.
- Example: To find the HCF of 15 and 30
Product of Two Numbers = HCF X LCM of the Two Numbers
- For any two positive integers a and b,
a×b=H.C.F×L.C.M. - Example – For 36 and 56, the H.C.F is 4 and the L.C.M is 504
36×56=2016
4×504=2016
Thus, 36×56=4×504 - Let us consider another example:
For 5 and 6, the H.C.F is 1 and the L.C.M is 30
5 × 6 = 30
1 × 30 =30
Thus, 5 × 6 = 1 × 30 - The above relationship, however, doesn’t hold true for 3 or more numbers
Real Numbers
Exercise 1.1
Page: 7
1. Use Euclid’s division algorithm to find the HCF of:
i. 135 and 225
ii. 196 and 38220
iii. 867 and 255
Solutions:
i. 135 and 225
As you can see, from the question 225 is greater than 135. Therefore, by Euclid’s division algorithm, we have,
225 = 135 × 1 + 90
Now, remainder 90 ≠ 0, thus again using division lemma for 90, we get,
135 = 90 × 1 + 45
Again, 45 ≠ 0, repeating the above step for 45, we get,
90 = 45 × 2 + 0
The remainder is now zero, so our method stops here. Since, in the last step, the divisor is 45, therefore, HCF (225,135) = HCF (135, 90) = HCF (90, 45) = 45.
Hence, the HCF of 225 and 135 is 45.
ii. 196 and 38220
In this given question, 38220>196, therefore the by applying Euclid’s division algorithm and taking 38220 as divisor, we get,
38220 = 196 × 195 + 0
We have already got the remainder as 0 here. Therefore, HCF(196, 38220) = 196.
Hence, the HCF of 196 and 38220 is 196.
iii. 867 and 255
As we know, 867 is greater than 255. Let us apply now Euclid’s division algorithm on 867, to get,
867 = 255 × 3 + 102
Remainder 102 ≠ 0, therefore taking 255 as divisor and applying the division lemma method, we get,
255 = 102 × 2 + 51
Again, 51 ≠ 0. Now 102 is the new divisor, so repeating the same step we get,
102 = 51 × 2 + 0
The remainder is now zero, so our procedure stops here. Since, in the last step, the divisor is 51, therefore, HCF (867,255) = HCF(255,102) = HCF(102,51) = 51.
Hence, the HCF of 867 and 255 is 51.
2. Show that any positive odd integer is of the form 6q + 1, or 6q + 3, or 6q + 5, where q is some integer.
Solution:
Let a be any positive integer and b = 6. Then, by Euclid’s algorithm, a = 6q + r, for some integer q ≥ 0, and r = 0, 1, 2, 3, 4, 5, because 0≤r<6.
Now substituting the value of r, we get,
If r = 0, then a = 6q
Similarly, for r= 1, 2, 3, 4 and 5, the value of a is 6q+1, 6q+2, 6q+3, 6q+4 and 6q+5, respectively.
If a = 6q, 6q+2, 6q+4, then a is an even number and divisible by 2. A positive integer can be either even or odd Therefore, any positive odd integer is of the form of 6q+1, 6q+3 and 6q+5, where q is some integer.
3. An army contingent of 616 members is to march behind an army band of 32 members in a parade. The two groups are to march in the same number of columns. What is the maximum number of columns in which they can march?
Solution:
Given,
Number of army contingent members=616
Number of army band members = 32
If the two groups have to march in the same column, we have to find out the highest common factor between the two groups. HCF(616, 32), gives the maximum number of columns in which they can march.
By Using Euclid’s algorithm to find their HCF, we get,
Since, 616>32, therefore,
616 = 32 × 19 + 8
Since, 8 ≠ 0, therefore, taking 32 as new divisor, we have,
32 = 8 × 4 + 0
Now we have got remainder as 0, therefore, HCF (616, 32) = 8.
Hence, the maximum number of columns in which they can march is 8.
4. Use Euclid’s division lemma to show that the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
Solutions:
Let x be any positive integer and y = 3.
By Euclid’s division algorithm, then,
x = 3q + r for some integer q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
Therefore, x = 3q, 3q+1 and 3q+2
Now as per the question given, by squaring both the sides, we get,
x2 = (3q)2 = 9q2 = 3 × 3q2
Let 3q2 = m
Therefore, x2= 3m ……………………..(1)
x2 = (3q + 1)2 = (3q)2+12+2×3q×1 = 9q2 + 1 +6q = 3(3q2+2q) +1
Substitute, 3q2+2q = m, to get,
x2= 3m + 1 ……………………………. (2)
x2= (3q + 2)2 = (3q)2+22+2×3q×2 = 9q2 + 4 + 12q = 3 (3q2 + 4q + 1)+1
Again, substitute, 3q2+4q+1 = m, to get,
x2= 3m + 1…………………………… (3)
Hence, from equation 1, 2 and 3, we can say that, the square of any positive integer is either of the form 3m or 3m + 1 for some integer m.
5. Use Euclid’s division lemma to show that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Solution:
Let x be any positive integer and y = 3.
By Euclid’s division algorithm, then,
x = 3q+r, where q≥0 and r = 0, 1, 2, as r ≥ 0 and r < 3.
Therefore, putting the value of r, we get,
x = 3q
or
x = 3q + 1
or
x = 3q + 2
Now, by taking the cube of all the three above expressions, we get,
Case (i): When r = 0, then,
x2= (3q)3 = 27q3= 9(3q3)= 9m; where m = 3q3
Case (ii): When r = 1, then,
x3 = (3q+1)3 = (3q)3 +13+3×3q×1(3q+1) = 27q3+1+27q2+9q
Taking 9 as common factor, we get,
x3 = 9(3q3+3q2+q)+1
Putting = m, we get,
Putting (3q3+3q2+q) = m, we get ,
x3 = 9m+1
Case (iii): When r = 2, then,
x3 = (3q+2)3= (3q)3+23+3×3q×2(3q+2) = 27q3+54q2+36q+8
Taking 9 as common factor, we get,
x3=9(3q3+6q2+4q)+8
Putting (3q3+6q2+4q) = m, we get ,
x3 = 9m+8
Therefore, from all the three cases explained above, it is proved that the cube of any positive integer is of the form 9m, 9m + 1 or 9m + 8.
Exercise 1.2 Page: 11
1. Express each number as a product of its prime factors:
(i) 140
(ii) 156
(iii) 3825
(iv) 5005
(v) 7429
Solutions:
(i) 140
By Taking the LCM of 140, we will get the product of its prime factor.
Therefore, 140 = 2 × 2 × 5 × 7 × 1 = 22×5×7
(ii) 156
By Taking the LCM of 156, we will get the product of its prime factor.
Hence, 156 = 2 × 2 × 13 × 3 × 1 = 22× 13 × 3
(iii) 3825
By Taking the LCM of 3825, we will get the product of its prime factor.
Hence, 3825 = 3 × 3 × 5 × 5 × 17 × 1 = 32×52×17
(iv) 5005
By Taking the LCM of 5005, we will get the product of its prime factor.
Hence, 5005 = 5 × 7 × 11 × 13 × 1 = 5 × 7 × 11 × 13
(v) 7429
By Taking the LCM of 7429, we will get the product of its prime factor.
Hence, 7429 = 17 × 19 × 23 × 1 = 17 × 19 × 23
2. Find the LCM and HCF of the following pairs of integers and verify that LCM × HCF = product of the two numbers.
(i) 26 and 91
(ii) 510 and 92
(iii) 336 and 54
Solutions:
(i) 26 and 91
Expressing 26 and 91 as product of its prime factors, we get,
26 = 2 × 13 × 1
91 = 7 × 13 × 1
Therefore, LCM (26, 91) = 2 × 7 × 13 × 1 = 182
And HCF (26, 91) = 13
Verification
Now, product of 26 and 91 = 26 × 91 = 2366
And Product of LCM and HCF = 182 × 13 = 2366
Hence, LCM × HCF = product of the 26 and 91.
(ii) 510 and 92
Expressing 510 and 92 as product of its prime factors, we get,
510 = 2 × 3 × 17 × 5 × 1
92 = 2 × 2 × 23 × 1
Therefore, LCM(510, 92) = 2 × 2 × 3 × 5 × 17 × 23 = 23460
And HCF (510, 92) = 2
Verification
Now, product of 510 and 92 = 510 × 92 = 46920
And Product of LCM and HCF = 23460 × 2 = 46920
Hence, LCM × HCF = product of the 510 and 92.
(iii) 336 and 54
Expressing 336 and 54 as product of its prime factors, we get,
336 = 2 × 2 × 2 × 2 × 7 × 3 × 1
54 = 2 × 3 × 3 × 3 × 1
Therefore, LCM(336, 54) = = 3024
And HCF(336, 54) = 2×3 = 6
Verification
Now, product of 336 and 54 = 336 × 54 = 18,144
And Product of LCM and HCF = 3024 × 6 = 18,144
Hence, LCM × HCF = product of the 336 and 54.
3. Find the LCM and HCF of the following integers by applying the prime factorisation method.
(i) 12, 15 and 21
(ii) 17, 23 and 29
(iii) 8, 9 and 25
Solutions:
(i) 12, 15 and 21
Writing the product of prime factors for all the three numbers, we get,
12=2×2×3
15=5×3
21=7×3
Therefore,
HCF(12,15,21) = 3
LCM(12,15,21) = 2 × 2 × 3 × 5 × 7 = 420
(ii) 17, 23 and 29
Writing the product of prime factors for all the three numbers, we get,
17=17×1
23=23×1
29=29×1
Therefore,
HCF(17,23,29) = 1
LCM(17,23,29) = 17 × 23 × 29 = 11339
(iii) 8, 9 and 25
Writing the product of prime factors for all the three numbers, we get,
8=2×2×2×1
9=3×3×1
25=5×5×1
Therefore,
HCF(8,9,25)=1
LCM(8,9,25) = 2×2×2×3×3×5×5 = 1800
4. Given that HCF (306, 657) = 9, find LCM (306, 657).
Solution: As we know that,
HCF×LCM=Product of the two given numbers
Therefore,
9 × LCM = 306 × 657
LCM = (306×657)/9 = 22338
Hence, LCM(306,657) = 22338
5. Check whether 6n can end with the digit 0 for any natural number n.
Solution: If the number 6n ends with the digit zero (0), then it should be divisible by 5, as we know any number with unit place as 0 or 5 is divisible by 5.
Prime factorization of 6n = (2×3)n
Therefore, the prime factorization of 6n doesn’t contain prime number 5.
Hence, it is clear that for any natural number n, 6n is not divisible by 5 and thus it proves that 6n cannot end with the digit 0 for any natural number n.
6. Explain why 7 × 11 × 13 + 13 and 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 are composite numbers.
Solution: By the definition of composite number, we know, if a number is composite, then it means it has factors other than 1 and itself. Therefore, for the given expression;
7 × 11 × 13 + 13
Taking 13 as common factor, we get,
=13(7×11×1+1) = 13(77+1) = 13×78 = 13×3×2×13
Hence, 7 × 11 × 13 + 13 is a composite number.
Now let’s take the other number,
7 × 6 × 5 × 4 × 3 × 2 × 1 + 5
Taking 5 as a common factor, we get,
=5(7×6×4×3×2×1+1) = 5(1008+1) = 5×1009
Hence, 7 × 6 × 5 × 4 × 3 × 2 × 1 + 5 is a composite number.
7. There is a circular path around a sports field. Sonia takes 18 minutes to drive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point?
Solution: Since, Both Sonia and Ravi move in the same direction and at the same time, the method to find the time when they will be meeting again at the starting point is LCM of 18 and 12.
Therefore, LCM(18,12) = 2×3×3×2×1=36
Hence, Sonia and Ravi will meet again at the starting point after 36 minutes.
Exercise 1.3 Page: 14
1. Prove that √5 is irrational.
Solutions: Let us assume, that √5 is rational number.
i.e. √5 = x/y (where, x and y are co-primes)
y√5= x
Squaring both the sides, we get,
(y√5)2 = x2
⇒5y2 = x2……………………………….. (1)
Thus, x2 is divisible by 5, so x is also divisible by 5.
Let us say, x = 5k, for some value of k and substituting the value of x in equation (1), we get,
5y2 = (5k)2
⇒y2 = 5k2
is divisible by 5 it means y is divisible by 5.
Clearly, x and y are not co-primes. Thus, our assumption about √5 is rational is incorrect.
Hence, √5 is an irrational number.
2. Prove that 3 + 2√5 + is irrational.
Solutions: Let us assume 3 + 2√5 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 3 + 2√5 = x/y
Rearranging, we get,
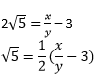
Since, x and y are integers, thus,
 is a rational number.
is a rational number.
Therefore, √5 is also a rational number. But this contradicts the fact that √5 is irrational.
So, we conclude that 3 + 2√5 is irrational.
3. Prove that the following are irrationals:
(i) 1/√2
(ii) 7√5
(iii) 6 + √2
Solutions:
(i) 1/√2
Let us assume 1/√2 is rational.
Then we can find co-prime x and y (y ≠ 0) such that 1/√2 = x/y
Rearranging, we get,
√2 = y/x
Since, x and y are integers, thus, √2 is a rational number, which contradicts the fact that √2 is irrational.
Hence, we can conclude that 1/√2 is irrational.
(ii) 7√5
Let us assume 7√5 is a rational number.
Then we can find co-prime a and b (b ≠ 0) such that 7√5 = x/y
Rearranging, we get,
√5 = x/7y
Since, x and y are integers, thus, √5 is a rational number, which contradicts the fact that √5 is irrational.
Hence, we can conclude that 7√5 is irrational.
(iii) 6 +√2
Let us assume 6 +√2 is a rational number.
Then we can find co-primes x and y (y ≠ 0) such that 6 +√2 = x/y⋅
Rearranging, we get,
√2 = (x/y) – 6
Since, x and y are integers, thus (x/y) – 6 is a rational number and therefore, √2 is rational. This contradicts the fact that √2 is an irrational number.
Hence, we can conclude that 6 +√2 is irrational.
Exercise 1.4 Page: 17
1. Without actually performing the long division, state whether the following rational numbers will have a terminating decimal expansion or a non-terminating repeating decimal expansion:
(i) 13/3125 (ii) 17/8 (iii) 64/455 (iv) 15/1600 (v) 29/343 (vi) 23/(2352) (vii) 129/(225775) (viii) 6/15 (ix) 35/50 (x) 77/210
Solutions:
Note: If the denominator has only factors of 2 and 5 or in the form of 2m ×5n then it has terminating decimal expansion.
If the denominator has factors other than 2 and 5 then it has a non-terminating decimal expansion.
(i) 13/3125
Factorizing the denominator, we get,
3125 = 5 × 5 × 5 × 5 × 5 = 55
Since, the denominator has only 5 as its factor, 13/3125 has a terminating decimal expansion.
(ii) 17/8
Factorizing the denominator, we get,
8 = 2×2×2 = 23
Since, the denominator has only 2 as its factor, 17/8 has a terminating decimal expansion.
(iii) 64/455
Factorizing the denominator, we get,
455 = 5×7×13
Since, the denominator is not in the form of 2m × 5n, thus 64/455 has a non-terminating decimal expansion.
(iv) 15/ 1600
Factorizing the denominator, we get,
1600 = 26×52
Since, the denominator is in the form of 2m × 5n, thus 15/1600 has a terminating decimal expansion.
(v) 29/343
Factorizing the denominator, we get,
343 = 7×7×7 = 73 Since, the denominator is not in the form of 2m × 5n thus 29/343 has a non-terminating decimal expansion.
(vi)23/(2352)
Clearly, the denominator is in the form of 2m × 5n.
Hence, 23/ (2352) has a terminating decimal expansion.
(vii) 129/(225775)
As you can see, the denominator is not in the form of 2m × 5n.
Hence, 129/ (225775) has a non-terminating decimal expansion.
(viii) 6/15
6/15 = 2/5
Since, the denominator has only 5 as its factor, thus, 6/15 has a terminating decimal expansion.
(ix) 35/50
35/50 = 7/10
Factorising the denominator, we get,
10 = 2 × 5
Since, the denominator is in the form of 2m × 5n thus, 35/50 has a terminating decimal expansion.
(x) 77/210
77/210 = (7× 11)/ (30 × 7) = 11/30
Factorising the denominator, we get,
30 = 2 × 3 × 5
As you can see, the denominator is not in the form of 2m × 5n .Hence, 77/210 has a non-terminating decimal expansion.
2. Write down the decimal expansions of those rational numbers in Question 1 above which have terminating decimal expansions.
Solutions:
(i) 13/3125

13/3125 = 0.00416
(ii) 17/8
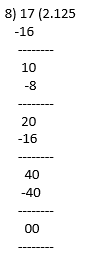
17/8 = 2.125
(iii) 64/455 has a Non terminating decimal expansion
(iv)15/ 1600

15/1600 = 0.009375
(v) 29/ 343 has a Non terminating decimal expansion
(vi)23/ (2352) = 23/(8×25)= 23/200

23/ (2352) = 0.115
(vii) 129/ (225775) has a Non terminating decimal expansion
(viii) 6/15 = 2/5

(ix) 35/50 = 7/10
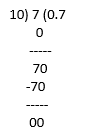
35/50 = 0.7
(x) 77/210 has a non-terminating decimal expansion.
3. The following real numbers have decimal expansions as given below. In each case, decide whether they are rational or not. If they are rational, and of the form, p q what can you say about the prime factors of q?
(i) 43.123456789
(ii) 0.120120012000120000. . .
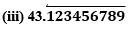
Solutions:
(i) 43.123456789
Since it has a terminating decimal expansion, it is a rational number in the form of p/q and q has factors of 2 and 5 only.
(ii) 0.120120012000120000. . .
Since, it has non-terminating and non- repeating decimal expansion, it is an irrational number.
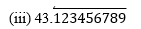
EXTRA QS
1. Find the HCF of 52 and 117 and express it in form 52x + 117y.
2. Prove that x2 – x is divisible by 2 for all positive integer x.
3. If m and n are odd positive integers, then m2 + n2 is even, but not divisible by 4. Justify.
4. If HCF (6, a) = 2 and LCM (6, a) = 60, then find a.
5. If remainder of

is a natural number, then find it.
6. If n is any prime number and a2 is divisible by n, then n will also divide a. Justify.
7. Find the missing numbers in prime factors tree.
8. Find the greatest number of 5 digits exactly divisible by 12, 15 and 36.
9. Find the smallest number which when increased by 20 is exactly divisible by 90 and 144.
10. Find the smallest number which leaves remainder 8 and 12 when divided by 28 and 32 respectively.
11. Floor of a room is to be fitted with square marble tiles of the largest possible size. The size of the room is 10 m × 7 m. What should be the size of tiles required that has to be cut and how many such tiles are required?
12. If the HCF of 408 and 1032 is expressible in the form 1032p – 408 × 5 find p.
1. Has the rational number

a terminating or a non-terminating decimal representation?
2. Prove that

is an irrational number.
3. (i) Find the LCM and HCF of 120 and 144 by using Fundamental Theorem of Arithmetic.
(ii)

find the values of m and n where m and n are non-negative integers.
Hence write its decimal expansion without actual division.
4. Prove that

is irrational.
5. Express the number

in the form of rational number

6. The LCM of 2 numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one number is 280, then find the other number.
7. The decimal expansion of π is:
(a) terminating
(b) non-terminating and non-recurring
(c) non-terminating and recurring
(d) doesn’t exist
8. Which of the following rational numbers have a terminating decimal expansion?
9. If the HCF of 55 and 99 is expressible in the form 55m 99, then the value of m is:
10. Given that LCM (91, 26) = 182, then HCF (91, 26) is:
1. Has the rational number

a terminating or a non-terminating decimal representation?
2. Prove that

is an irrational number.
3. (i) Find the LCM and HCF of 120 and 144 by using Fundamental Theorem of Arithmetic.
(ii)

find the values of m and n where m and n are non-negative integers.
Hence write its decimal expansion without actual division.
4. Prove that

is irrational.
5. Express the number

in the form of rational number

6. The LCM of 2 numbers is 14 times their HCF. The sum of LCM and HCF is 600. If one
number is 280, then find the other number.
7. The decimal expansion of π is:
(a) terminating
(b) non-terminating and non-recurring
(c) non-terminating and recurring
(d) doesn’t exist
8. Which of the following rational numbers have a terminating decimal expansion?
9. If the HCF of 55 and 99 is expressible in the form 55m 99, then the value of m is:
10. Given that LCM (91, 26) = 182, then HCF (91, 26) is:
(a) 13
(b) 26
(c) 7
1. The decimal expansion of number

has:
(a) a terminating decimal
(b) non-terminating but repeating
(c) non-terminating non repeating
(d) terminating after two places of decimal
2. The values of x and y in the given figure are:

(a) x = 10; y = 14
(b) x = 21; y = 84
(c) x = 21; y = 25
(d) x = 10; y = 40
3. For any positive integer a and 3, there exist unique integers q and r such that a = 3q + r, where r must satisfy :
(a) 0 ≤ r < 3
(b) 1 < r < 3
(c) 0 < r < 3
(d) 0 < r ≤ 3
4. 
is:
(a) a rational number
(b) an irrational number
(c) a prime number
(d) an even number
5. L.C.M. of 23 × 32 and 22 × 33 is :
(a) 23
(b) 33
(c) 23 × 33
(d) 22 × 32
6. The HCF and LCM of two numbers are 33 and 264 respectively. When the first number is completely divided by 2 the quotient is 33. The other number is:
(a) 66
(b) 130
(c) 132
(d) 196
7. What will be the least possible number of the planks, if three pieces of timber 42 m, 49 m and 63 m long have to be divided into planks of the same length?
(a) 5
(b) 6
(c) 7
(d) none of these
8. What is the greatest possible speed at which a man can walk 52 km and 91 km in an exact number of minutes?
(a) 17 m/min
(b) 7 m/min
(c) 13 m/min
(d) 26 m/min
9. If A = 2n + 13, B = n + 7, where n is a natural number then HCF of A and B is:
10. Pairs of natural numbers whose least common multiple is 78 and the greatest common divisor is 13 are:
(a) 58 and 13 or 16 and 29
(b) 68 and 23 or 36 and 49
(c) 18 and 73 or 56 and 93
(d) 78 and 13 or 26 and 39
11. Two natural numbers whose sum is 85 and the least common multiple is 102 are:
(a) 30 and 55
(b) 17 and 68
(c) 35 and 55
(d) 51 and 34
12. 4 Bells toll together at 9.00 am. They toll after 7, 8, 11 and 12 seconds respectively. How many times will they toll together again in the next 3 hours?
13. A forester wants to plant 66 apple trees, 88 banana trees and 110 mango trees in equal rows (in terms of number of trees). Also he wants to make distinct rows of trees (i.e., only one type of trees in one row). The number of minimum rows required are
14. A number 10x + y is multiplied by another number 10a + b and the result comes as 100p + 10q +r, where r = 2y, q = 2(x + y) and p = 2x; x, y < 5, q ≠ 0. The value of 10a + b may be:
15. If the HCF of 65 and 117 is expressible in the form 65m – 117, then the value of m is
16. The largest number which divides 70 and 125, leaving remainders 5 and 8 respectively, is
(a) 13
(b) 65
(c) 875
(d) 1750
17. If two positive integers a and b are written as a = x3y2 and b = xy3; x, y are prime numbers, then HCF (a, b) is
(a) xy
(b) xy2
(c) x3y3
(d) x2y2
18. If two positive integers p and q can be expressed as p = ab2 and q = a3b; a, b being prime numbers, then LCM (p, q) is
(a) ab
(b) a2b2
(c) a3b2
(d) a3b3
19. The least number that is divisible by all the numbers from 1 to 10 (both inclusive) is
(a) 10
(b) 100
(c) 504
(d) 2520
20. The decimal expansion of the rational number

will terminate after
(a) one decimal place
(b) two decimal places
(c) three decimal places
(d) four decimal places
| 1. (a) | 2. (b) | 3. (a) | 4. (b) | 5. (c) |
| 6. (c) | 7. (d) | 8. (c) | 9. (b) | 10 (d) |
| 11. (d) | 12. (c) | 13. (d) | 14. (d) | 15. (b) |
| 16. (a) | 17. (b) | 18. (c) | 19. (d) | 20. (d) |


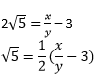
 is a rational number.
is a rational number.